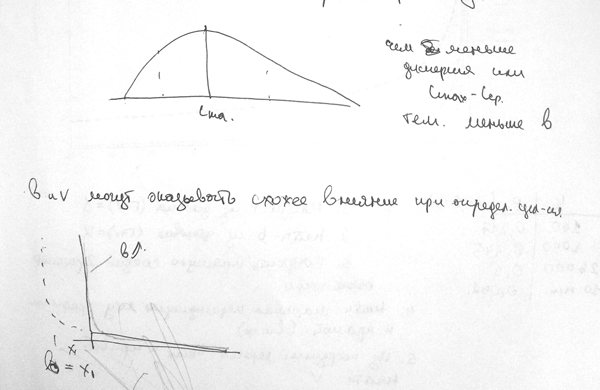Некоторое время назад я со своими аспирантками Ириной Голубевой и Мариной Даньшиной подготовили задание для исследования частотных закономерностей в музыке на примере знаменных песнопений. Подробнее см. на страничке проекта Компьютерная семиография.
Закон Ципфа-Мандельброта для музыки
Теоретической базой для проведения исследования являются материалы, представленные в разделе 2.1 «Количественная спецификация ЕЯ описания» Монографии Ю.Филиппович, А.Прохоров. Семантика информационных технологий: опыты словарно- тезаурусного описания. / Серия «Компьютерная лингвистика». Вступ. Статья А.И.Новикова. М.: МГУП, 2002.— книга в комплекте с CD ROM.
Там приводятся описания законов Ципфа и Мандельброта, которые эмпирически установили формы гиперболических зависимостей частоты употребления слов в текстах. Позднее аналогичные зависимости были обнаружены и в других областях коммуникации и человеческой деятельности. Думаю, что кто-то, наверняка, это подтвердил и для музыкальных произведений.
В нашем исследовании мы рассматриваем особый класс музыкальных произведений (древнерусские знаменные песнопения), которые имеют ряд отличительных особенностей, в том числе явно выраженную компонентную структуру организации мелодий. Для современной ното-линейной (фактически, фонетической) записи выделение структурных единиц в общем случае неочевидно и неоднозначно, поэтому исследователи часто используют N-граммные модели и разбивают мелодии на равные фрагменты по три-четыре ноты.
Теоретически такое равномерное разбиение должно приводить к отклонениям от законов Ципфа-Мандельброта, т.к. статистически выявлено, что более короткие слова чаще употребляются и чаще носят служебный характер. В знаменных же песнопениях простейшим музыкальным единицам (семиографическим знакам, знаменам, крюкам) могут соответствовать различные по длительности последовательности, что делает их исследование с помощью соответствующих инструментов более обоснованным. В скором времени, я надеюсь, что мы сможем представить наши официальные результаты, которые мы в настоящее время проверяем на дополнительных данных, детализируем и т.д.
Расчет коэффициентов закона Мандельброта
В этом же посте я хочу поделиться некоторыми своими соображениями и даже расчетами по определению коэффициентов формул Ципфа-Мандельброта. Для этого я специально перерыл старые документы и нашел свои записи десятилетней давности. Наверняка, на сегодняшний день, когда компьютерной лингвистикой не занимается только ленивый, в Интернете могут быть найдены более серьезные выкладки или даже исследования на эту тему. Буду признателен за ссылки ))
Хочу также попросить прощения за «ручной» формат представления выкладок, т.к. на текущий момент Mathcad на компьютере у меня не установлен и скриншоты могу сделать только со старых распечаток.
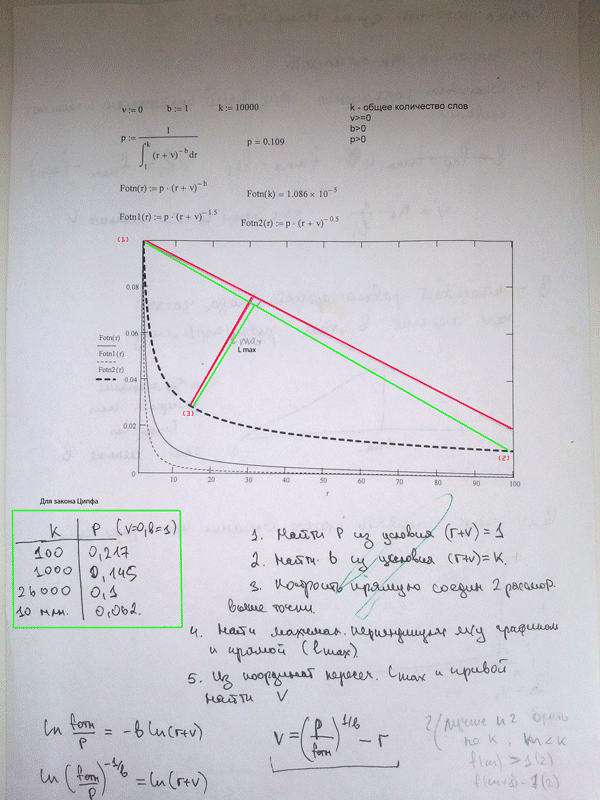
На «скриншоте» в верхней части представлены формулы Mathcad для расчета коэффициентов, графики и некоторые пояснения:
- Fotn – относительная частота встречаемости слов (знамен или других единиц). Нормировка (собственно относительность рассчитывается исходя из деления абсолютной частоты на общее количество слов k, рангов).
- Fotn (r) – Закон Ципфа (b=1, v=0)
- Fotn1 (r), Fotn2 (r) – Закон Мандельброта (b=1,5 и b=0,5; v=0)
В левой части под рисунком представлены результаты расчета коэффициента p для Закона Ципфа. Можно увидеть, что 1/10 получается только при общем количестве слов (рангов) около 26000.
Методика расчета довольно проста:
- Найти p из условия, что (r+v)=1. На графике это точка, отмеченная красной цифрой (1).
- Найти b из условия (r+v)=k. Но лучше выбрать не к, а m такое, что m<k, абсолютная частота F(m )>1. Это позволяет не брать в расчет хвост единичных случаев. На графике это точка, отмеченная красной цифрой (2). К одной точке ведет красная линия, а к другой – зеленая. Линии показаны условно.
- Найти самую характерную точку изгиба кривой и для нее вычислить v
- Соединить прямой рассмотренные выше точки (1) и (2)
- Найти максимальный перпендикуляр Lmax между прямой и кривой. Желающие могут сделать формальную запись поиска экстремума соответствующей функции ))
- Из координат пересечения (3) найти v по формуле
v=(p/Fотн)^(1/b)-r.
«Физический смысл» коэффициентов закона Мандельброта
- P — это максимальная относительная частота слова (знамени).
- V – показывает соотношение между наиболее и наименее частотными словами (знаменами):
- Если ввести коэффициент U= Fmax—Fmin или U1=Fmax—Favg, то он будет обратно пропорционален V, т.е.:
- Чем больше U, тем меньше V : V=a1*(1/U)
- B – показывает равномерность спада частот – чем меньше B, тем равномерней спад. Соответственно, чем меньше дисперсия, тем меньше B.
Вопрос о правильном определении ранга
При построении реально наблюдаемой модели ранг-частота можно словам (знаменам) с одинаковой частотой присваивать одинаковый ранг, можно даже этот принцип распространить на диапазоны частот. Это приведет к тому, что функция распределения будет носить более «ступенчатый характер», а ее сглаживание непрерывной функцией будет в общем случае сложней или менее правдоподобней. Соответственно, для теоретических расчетов лучше каждому слову (знамени) присваивать отдельный ранг, а в практических задачах количество рангов определять из стоящих перед разработчиком (исследователем) задач.